
Zadanie Kupno gruntu (kup)
Pomóż nam usprawnić bazę zadań!
Kupno gruntu
Limit pamięci: 64 MB
Bajtazar planuje kupno działki przemysłowej.
Jego majątek jest wyceniany na 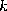 bajtalarów.
Tyle też zamierza on przeznaczyć na zakup gruntu.
Jednak znalezienie działki, która kosztuje dokładnie
bajtalarów.
Tyle też zamierza on przeznaczyć na zakup gruntu.
Jednak znalezienie działki, która kosztuje dokładnie 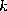 bajtalarów, jest kłopotliwe.
W związku z tym, Bajtazar jest gotów kupić ewentualnie droższą działkę.
Dodatkowe fundusze może uzyskać przez zaciągnięcie kredytu.
Maksymalny rozmiar kredytu, jaki może mu udzielić Bajtocki Bank Kredytowy,
wynosi tyle, ile majątek Bajtazara, czyli
bajtalarów, jest kłopotliwe.
W związku z tym, Bajtazar jest gotów kupić ewentualnie droższą działkę.
Dodatkowe fundusze może uzyskać przez zaciągnięcie kredytu.
Maksymalny rozmiar kredytu, jaki może mu udzielić Bajtocki Bank Kredytowy,
wynosi tyle, ile majątek Bajtazara, czyli 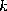 bajtalarów.
Innymi słowy, Bajtazar chciałby przeznaczyć na kupno działki kwotę w wysokości
od
bajtalarów.
Innymi słowy, Bajtazar chciałby przeznaczyć na kupno działki kwotę w wysokości
od 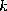 bajtalarów do
bajtalarów do 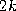 bajtalarów włącznie.
bajtalarów włącznie.
Teren, na którym Bajtazar zamierza kupić działkę, ma kształt kwadratu o boku długości  metrów.
Aktualni właściciele ziemi wyznaczyli różne ceny w przeliczeniu na metr kwadratowy.
Bajtazar przeprowadził dokładny wywiad i sporządził mapę cenową tego terenu.
Mapa ta opisuje cenę każdego kwadratu o rozmiarze metr na metr.
Takich kwadratów jest dokładnie
metrów.
Aktualni właściciele ziemi wyznaczyli różne ceny w przeliczeniu na metr kwadratowy.
Bajtazar przeprowadził dokładny wywiad i sporządził mapę cenową tego terenu.
Mapa ta opisuje cenę każdego kwadratu o rozmiarze metr na metr.
Takich kwadratów jest dokładnie 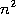 .
Teraz pozostaje wyznaczyć wymarzoną działkę.
Musi ona mieć kształt prostokąta, złożonego wyłącznie z całych kwadratów jednostkowych.
Bajtazar zaczął szukać na mapie odpowiedniej działki,
ale mimo wzmożonych wysiłków nie był w stanie znaleźć właściwego prostokąta.
Pomóż Bajtazarowi.
.
Teraz pozostaje wyznaczyć wymarzoną działkę.
Musi ona mieć kształt prostokąta, złożonego wyłącznie z całych kwadratów jednostkowych.
Bajtazar zaczął szukać na mapie odpowiedniej działki,
ale mimo wzmożonych wysiłków nie był w stanie znaleźć właściwego prostokąta.
Pomóż Bajtazarowi.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia liczby
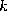 i
i  oraz mapę cenową terenu,
oraz mapę cenową terenu,
- wyznaczy działkę o cenie z przedziału
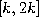 lub stwierdzi, że taka działka nie istnieje,
lub stwierdzi, że taka działka nie istnieje,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite 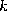 i
i  oddzielone pojedynczym odstępem,
oddzielone pojedynczym odstępem, 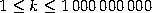 ,
, 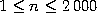 .
Każdy z następnych
.
Każdy z następnych  wierszy zawiera
wierszy zawiera  liczb całkowitych nieujemnych,
pooddzielanych pojedynczymi odstępami.
liczb całkowitych nieujemnych,
pooddzielanych pojedynczymi odstępami.
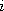 -ta liczba w wierszu numer
-ta liczba w wierszu numer  określa cenę jednego kwadratu metr na metr,
którego współrzędne w terenie to
określa cenę jednego kwadratu metr na metr,
którego współrzędne w terenie to 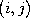 .
Cena jednego metra nie przekracza
.
Cena jednego metra nie przekracza 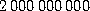 bajtalarów.
bajtalarów.
Wyjście
Jeżeli nie istnieje działka o cenie z przedziału 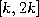 ,
to program powinien wypisać jeden wiersz zawierający słowo NIE.
W przeciwnym przypadku powinien wypisać jeden wiersz zawierający cztery liczby
całkowite dodatnie
,
to program powinien wypisać jeden wiersz zawierający słowo NIE.
W przeciwnym przypadku powinien wypisać jeden wiersz zawierający cztery liczby
całkowite dodatnie 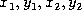 pooddzielane pojedynczymi odstępami, określające współrzędne prostokąta.
pooddzielane pojedynczymi odstępami, określające współrzędne prostokąta.
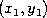 oznaczają lewy górny róg prostokąta, a
oznaczają lewy górny róg prostokąta, a 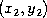 prawy dolny róg prostokąta.
Wtedy taki prostokąt określony jest przez zbiór współrzędnych kwadratów:
prawy dolny róg prostokąta.
Wtedy taki prostokąt określony jest przez zbiór współrzędnych kwadratów:
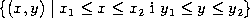 .
Suma cen kwadratów
.
Suma cen kwadratów  leżących wewnątrz wskazanego prostokąta powinna spełniać
nierówności
leżących wewnątrz wskazanego prostokąta powinna spełniać
nierówności 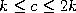 .
Jeżeli jest więcej działek spełniających wymagany warunek,
to należy wypisać dowolną z nich.
.
Jeżeli jest więcej działek spełniających wymagany warunek,
to należy wypisać dowolną z nich.
Przykład
Dla danych wejściowych:
4 3 1 1 1 1 9 1 1 1 1
poprawną odpowiedzią jest:
NIE
a dla danych wejściowych:
8 4 1 2 1 3 25 1 2 1 4 20 3 3 3 30 12 2
poprawną odpowiedzią jest:
2 1 4 2
Autor zadania: Marcin Kubica.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English